Python
Linear regression offers a simple method for predicting student academic performance by examining the relationship between factors like study and sleep hours with educational outcomes. Its interpretability makes it a valuable tool for educators, enabling them to identify important factors influencing student success, make data-driven decisions, and provide targeted support to students who may be at risk. With its scalability and predictive capabilities, linear regression allows for continuous improvement in educational interventions, ultimately contributing to better student outcomes and learning experiences.
When I usually explore relationships between variables in a dataset, before performing the regression analysis, I like to create a correlation heatmap. As seen below, the correlation heatmap highlights the strength and type of relationship between variables. In this case, darker the blue, the weaker the relationship, darker the red, the stronger the relationship. Correlations help us to understand which variables has the highest potential of explaining the variance in the variable being predicted.
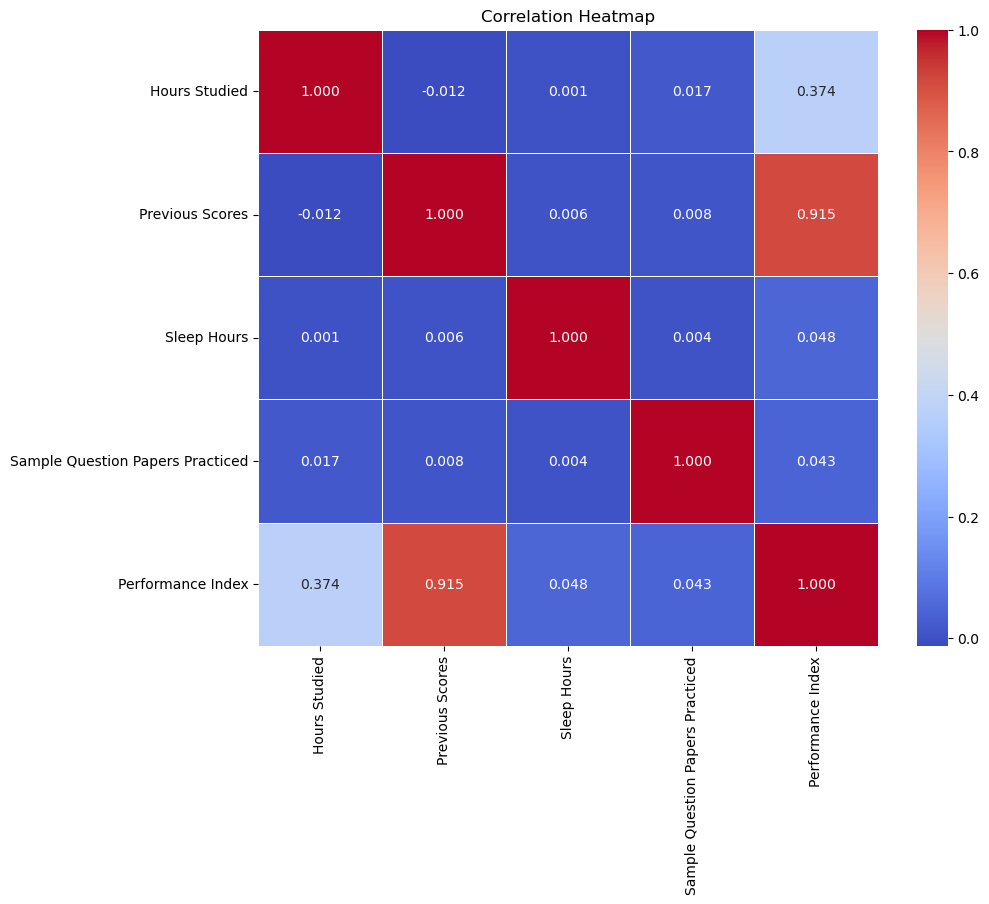
For this set of students, it seems the two strongest predictors would be previous scores and hours studied (in that order). For this analysis, I'll choose to take the strongest predictor, previous scores, in predicting student performance.
So, the results from the analysis tell us, that the model was a Multiple R of 0.83 (thats a quite a strong model), and using previous scores to predict a performance index, the intercept (-15.18) would represent the predicted performance index if the previous score was zero. The coefficient (1.01) would suggest that for every one-point increase in the previous score, the predicted performance index increases by about 1.01 points. The predicted performance indices [-14.67, -14.37, -13.97] would then be hypothetical predictions based on different previous scores, helping us understand how well our prediction model works in practice. Essentially, the model tells us how much previous scores can help us statistcally guess a student's performance index.
Here's the interesting part, if we dig deeper and aim to strengthen this model by adding "hours studied" as an additional independent variable, we can actually achieve a higher Multiple R of 0.98. This suggests a very strong model of prediction now, and so we should use this formula as a algorithm of prediction
Performance Index = −29.816789860385555+2.857637245414692 X Hours Studied + 1.0191227514123198 X Previous Scores
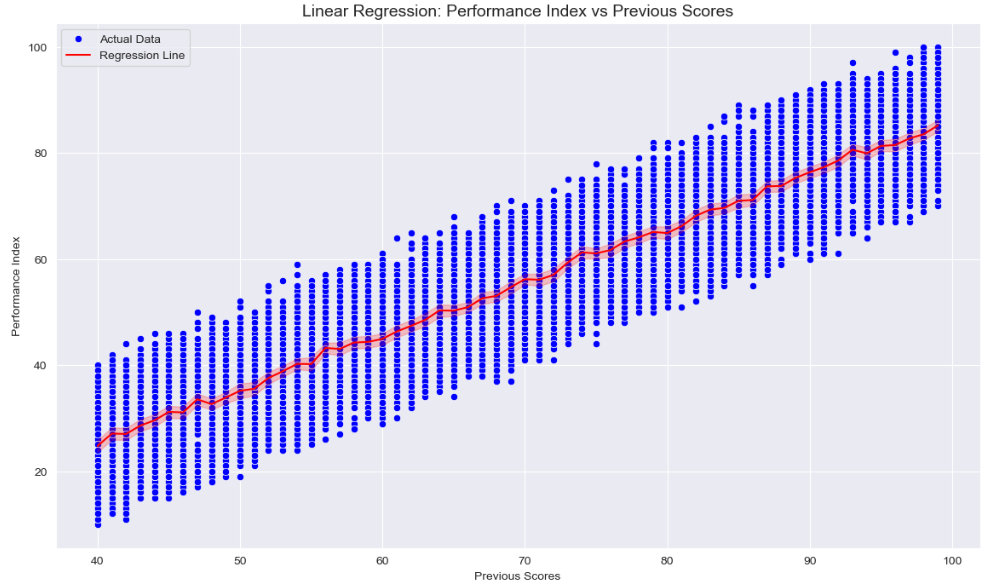
The importance of findings intepretation
Clear interpretation helps stakeholders understand the implications of the findings, enabling them to make informed decisions, devise effective strategies, and take appropriate actions. In this analysis, it was important to highlight the strong predicting power of previous scores, but another important factor is that hours studied also has the ability to strengthen our predictive model. This warrants and encourages further analysis to deepen our understanding of student performance.